Discursive dilemma
Discursive dilemma or doctrinal paradox is a paradox in social choice theory which states that aggregating judgements with majority voting might result in a self-contradictory judgement.
| P | Q | R = P & Q | R | |
|---|---|---|---|---|
| Judge 1 | yes | yes | yes | yes |
| Judge 2 | no | yes | yes | no |
| Judge 3 | yes | no | yes | no |
| Majority decision | yes | yes | yes | no |
Assume that a three-member court must decide whether someone is liable for a breach of contract. The judges have to decide which of the following propositions are true:
- P: the defendant did a certain action;
- Q: the defendant had a contractual obligation not to do that action;
- R: the defendant is liable.
Additionally, all judges accept the proposition 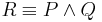 , which is the just legal doctrine that you are liable if you breach contract. Each judge makes a consistent (non-contradictory) judgement: they will accept R if and only if they accept both P and Q. As can be seen in the table, if they decide about each proposition by majority vote, the resulting judgement will not necessarily be consistent.
, which is the just legal doctrine that you are liable if you breach contract. Each judge makes a consistent (non-contradictory) judgement: they will accept R if and only if they accept both P and Q. As can be seen in the table, if they decide about each proposition by majority vote, the resulting judgement will not necessarily be consistent.
An actual decision-making procedure might be premise-based or conclusion-based. In a premise-based procedure, the judges decide by voting whether the conditions for liability are met. In a conclusion-based procedure, the judges decide directly whether the defendant should be liable. In this formulation, the paradox is that the two procedures don't necessarily lead to the same result.
The discursive dilemma can be seen as a generalization of the Condorcet paradox, as a preference set is just a special kind of proposition set. Just as the Condorcet paradox can be generalized to Arrow's theorem, List and Pettit argue that the discursive dilemma can be generalized to the List-Pettit theorem, which states that the inconsistency remains for any aggregation method which meets a few natural conditions.
References
- List, C. and Pettit, P.: Aggregating Sets of Judgments: Two Impossibility Results Compared, Synthese 140 (2004) 207–235
External links
- Judgment aggregation: an introduction and bibliography of the discursive dilemma by Christian List